Volver a Guía
Ir al curso
Para responder esta pregunta, vamos a usar que el área bajo la curva en el gráfico de velocidad en función del tiempo es el desplazamiento (es decir, $\Delta x$, el área coincide con cuánto se desplazó en ese intervalo de tiempo)
Reportar problema
CURSO RELACIONADO
Física 03
2026
TORTI
¿Te está ayudando la guía resuelta?
Sumate a nuestro curso, donde te enseño toda la materia de forma súper simple. 🥰
Ir al curso
FÍSICA 03 UBA XXI
CÁTEDRA TORTI
Unidad 4
1.
Una pelota se mueve en línea recta (eje $x$). En la gráfica muestra la velocidad de la pelota en función del tiempo.
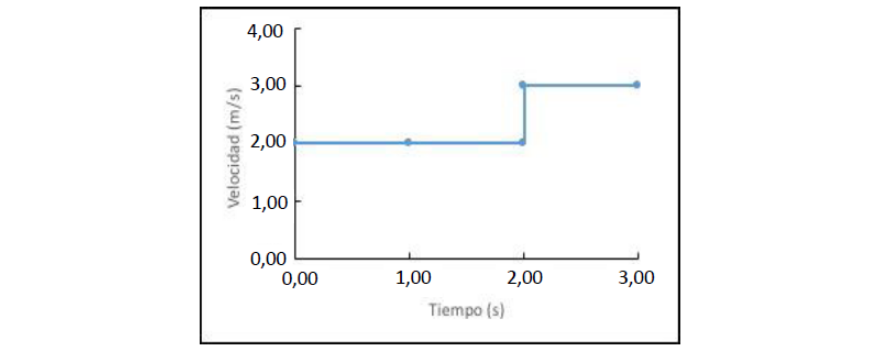
a) ¿Cuáles son la rapidez media y la velocidad media de la pelota durante los primeros $3,00 \mathrm{~s}$?

a) ¿Cuáles son la rapidez media y la velocidad media de la pelota durante los primeros $3,00 \mathrm{~s}$?
Respuesta
💡 Importante: Igual que te vengo recomendado en las guías anteriores, mi consejo es que veas primero las clases y resoluciones que fuimos haciendo en las clases de Cinemática y después vengas a estos ejercicios de la guía, para seguir practicando.
Ahora sí, arrancamos...
Sabemos que la velocidad media $(V_m)$ está definida por
$V_m = \frac{x_f - x_i}{t_f - ti} = \frac{\Delta x}{\Delta t}$
Nuestro objetivo va a ser entonces calcular el área bajo la curva, para así obtener $\Delta x$ y después poder calcular la velocidad media.
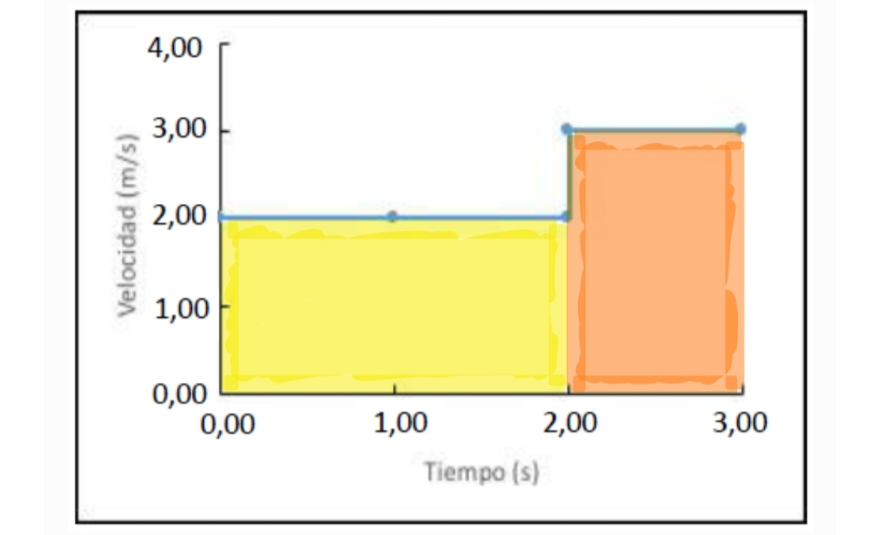
Mirando el gráfico, identificamos que tenemos dos rectángulos, de los cuales podemos calcular su área usando base x altura.
(El área bajo la curva que estamos buscando es justamente la suma del área amarilla + el área naranja)

Calculamos cada una de estas áreas:
Área amarilla -> Base: $2 \text{ s}$ / Altura: $2 \, \frac{m}{s}$ / El área es: $2 \text{ s} \cdot 2 \, \frac{m}{s} = 4 \text{ m}$
Área naranja -> Base: $1 \text{ s}$ / Altura: $3 \, \frac{m}{s}$ / El área es: $1 \text{ s} \cdot 3 \, \frac{m}{s} = 3 \text{ m}$
Con lo cual, el área bajo la curva para los primeros tres segundos es $4 \text{ m} + 3 \text{ m} = 7 \text{ m}$
Es decir, que en estos primeros $3$ segundos, la pelota se desplazó $7$ metros. Entonces, si ya sabemos que recorrió $7$ metros en $3$ segundos, podemos calcular su velocidad media:
$V_m = \frac{\Delta x}{\Delta t} = \frac{7 \text{ m}}{3 \text{ s}} = 2.33 \, \frac{m}{s}$
¡Perfectoooo! La velocidad media de la pelota en los primeros $3$ segundos fue de $2.33 \, \frac{m}{s}$
👉 Y acá justo en este ejercicio nos preguntan también por rapidez media, que no nos había aparecido hasta ahora, así que aprovechamos para discutirlo acá. La expresión para la rapidez media es similar a la de velocidad media, con la diferencia de que, en vez de usar el desplazamiento, usamos la distancia total recorrida.
En este caso, por ejemplo, la pelota se desplazó en total $7$ metros $(\Delta x)$ y eso coincide con la distancia total recorrida, claro, recorrió en total $7$ metros. Así que la rapidez media coincide con la velocidad media, es también $2.33 \, \frac{m}{s}$.
Pero eso no siempre es así -> Por ejemplo, si en un cierto intervalo de tiempo la pelota arrancó en un punto, recorrió $7$ metros y después volvió al punto de partida, la velocidad media es nula (porque $x_f$ y $x_i$ coinciden, la pelota empezó y terminó en el mismo punto, así que en ese intervalo de tiempo su desplazamiento fue nulo), en cambio su rapidez media no va a ser cero, porque la distancia total recorrida fueron 7 metros a la ida y 7 metros a la vuelta, en total recorrió 14 metros... ¿se ve la diferencia? Igual esto lo vamos a seguir trabajando en el próximo ítem, pasemos a ese ;)
🤖
¿Tenés dudas? Pregúntale a ExaBoti
Asistente de IA para resolver tus preguntas al instante🤖
¡Hola! Soy ExaBoti
Para chatear conmigo sobre este ejercicio necesitas iniciar sesión
ExaComunidad
Conecta con otros estudiantes y profesoresNo hay comentarios aún
¡Sé el primero en comentar!
